Making The XOR Perceptron

In my second post I wrote about perceptron and making a perceptron. And there I said that you can't make a XOR gate by using a perceptron, because a single perceptron can only do linearly separable problems. And XOR is not a linearly separable problem, so I thought of writing this post in how you can solve this.

I spent last couple of days, learning numpy and driving myself to insanity in how to make the two layer perceptron to solve the XOR gate problem. At one point I came to the verge of giving up, but the fun part of learning something by yourself not just in coding but anything is the feeling you get when you solve the problem, it's like finding a pot of gold at the end of the rainbow.

So how can you solve the XOR gate, it's by putting two input neurons, two hidden layer neurons and one output neuron all together using 5 neurons instead of just using one like we did it in the second post.

XOR perceptron structure

Although I call it a perceptron it's a miniature neural net itself, using backpropagation to learn. Just like what we did in the second post, we assign random values for the weights and we give the training data and the output, and we backpropagate until the error becomes minimum.

Few things that I learned the hard-way when making this was,

• Every value should go through activation when they pass through a neuron, even the inputs should pass through an activation function when they pass through the $i1$ and $i2$ neurons in the diagram, it took me sometime to figure this out by myself.
• In my second post I have used the positive value at the sigmoid function not the negative value, if using the positive value at the sigmoid function then the changes are added to the existing weights, but if you are using the negative value at the sigmioid function then the weight changes are deducted, form the existing weights. 
• You might have to run the learning process many rounds until you get to a point of acceptable error, because you might hit a local minimum where you can get close to the global minimum if you continue going through the training set.
• Also unlike in my second post it's better to calculate the total error, in the XOR there are four training sets, $[0,0],[0,1],[1,0],[1,1]$.
  So you run through the four training sets, add the error at each training set. So you will be adding up four errors ( $\sum E = 1/2 * (target \tiny i$ $ - output \tiny i )$ ), and then save that total error to graph not plotting or taking error at each training set in to account.

Also using python and numpy makes life lot simpler rather than using Node like I used in my second post in making the simple perceptron, as things get complex it's a must to use numpy and python andit will make your life way better, trust me.

And because I was learning numpy at the same time, there were times I got things wrong when using the dot multiplication. There were times like I said before I didn't ran the inputs through the activation function, which gave me all sorts of bizarre charts.

One bizarre chart I got when things were not going the right direction.

So after further reading, trial and error, calculating everything by hand and after finding them and fixing them

Calculating it manually

Finally saw the light at the end of the tunnel, after correcting all the error, the error came

Error changing (total error) per each round

As you can see I had to run many rounds unlike the previous single perceptron which reached to a acceptable minimum error around 10000 rounds I had to run this nearly the 13000+ rounds to get to a point where there is a drop in error (total error) also the learning rate ( $\eta$ ) was far less this time 0.25 compared to 0.5 in the previous example, that's one reason for it to take long time to get the correct weights.

Also as the starting weights are assigned randomly the learning rounds needed to reach to a reasonably low error can vary.

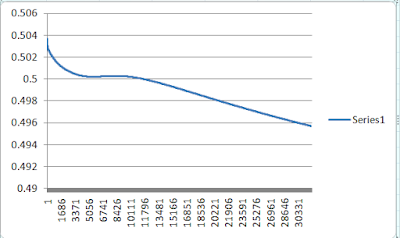
Although I can only plot 32000 rows in excel the error reached to 0.001009 by the time it reached 100,000 learning rounds.

And like here, there are times where it will never learn, this is because the weights are assigned randomly at the beginning. Even after 100,000 rounds the error has only reached 0.487738646. This might be due to the network has hit a local minimum and might work if we continue training it or it will just never learn.

You will never know whether a neural network will learn or not and what makes neural networks unpredictable.

I know making a XOR perceotron is no big deal as machine learning is light years ahead now. But the what matters is making something by yourself, and learning something out of it and the joy that you get at the end of reaching the destination.

I did not add any bias to this example like the previous one because I was having a tough time making this without the bias, but it's better to have a bias and will add
The code is available here - https://gist.github.com/rukshn/361a54eaec0266167051d2705ea08a5f