In my second post I wrote about perceptron and making a perceptron. And there I said that you can't make a XOR gate by using a perceptron, because a single perceptron can only do linearly separable problems. And XOR is not a linearly separable problem, so I thought of writing this post in how you can solve this.

I spent last couple of days, learning numpy and driving myself to insanity in how to make the two layer perceptron to solve the XOR gate problem. At one point I came to the verge of giving up, but the fun part of learning something by yourself not just in coding but anything is the feeling you get when you solve the problem, it's like finding a pot of gold at the end of the rainbow.

So how can you solve the XOR gate, it's by putting two input neurons, two hidden layer neurons and one output neuron all together using 5 neurons instead of just using one like we did it in the second post.

XOR perceptron structure

Although I call it a perceptron it's a miniature neural net itself, using backpropagation to learn. Just like what we did in the second post, we assign random values for the weights and we give the training data and the output, and we backpropagate until the error becomes minimum.

Few things that I learned the hard-way when making this was,

• Every value should go through activation when they pass through a neuron, even the inputs should pass through an activation function when they pass through the $i1$ and $i2$ neurons in the diagram, it took me sometime to figure this out by myself.
• In my second post I have used the positive value at the sigmoid function not the negative value, if using the positive value at the sigmoid function then the changes are added to the existing weights, but if you are using the negative value at the sigmioid function then the weight changes are deducted, form the existing weights. 
• You might have to run the learning process many rounds until you get to a point of acceptable error, because you might hit a local minimum where you can get close to the global minimum if you continue going through the training set.
• Also unlike in my second post it's better to calculate the total error, in the XOR there are four training sets, $[0,0],[0,1],[1,0],[1,1]$.
  So you run through the four training sets, add the error at each training set. So you will be adding up four errors ( $\sum E = 1/2 * (target \tiny i$ $ - output \tiny i )$ ), and then save that total error to graph not plotting or taking error at each training set in to account.

Also using python and numpy makes life lot simpler rather than using Node like I used in my second post in making the simple perceptron, as things get complex it's a must to use numpy and python andit will make your life way better, trust me.

And because I was learning numpy at the same time, there were times I got things wrong when using the dot multiplication. There were times like I said before I didn't ran the inputs through the activation function, which gave me all sorts of bizarre charts.

One bizarre chart I got when things were not going the right direction.

So after further reading, trial and error, calculating everything by hand and after finding them and fixing them

Calculating it manually

Finally saw the light at the end of the tunnel, after correcting all the error, the error came

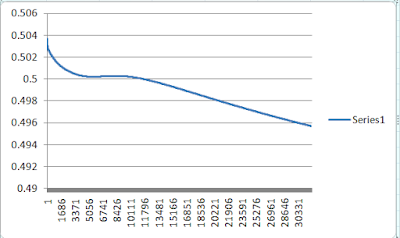
Error changing (total error) per each round

As you can see I had to run many rounds unlike the previous single perceptron which reached to a acceptable minimum error around 10000 rounds I had to run this nearly the 13000+ rounds to get to a point where there is a drop in error (total error) also the learning rate ( $\eta$ ) was far less this time 0.25 compared to 0.5 in the previous example, that's one reason for it to take long time to get the correct weights.

Also as the starting weights are assigned randomly the learning rounds needed to reach to a reasonably low error can vary.

Although I can only plot 32000 rows in excel the error reached to 0.001009 by the time it reached 100,000 learning rounds.

And like here, there are times where it will never learn, this is because the weights are assigned randomly at the beginning. Even after 100,000 rounds the error has only reached 0.487738646. This might be due to the network has hit a local minimum and might work if we continue training it or it will just never learn.

You will never know whether a neural network will learn or not and what makes neural networks unpredictable.

I know making a XOR perceotron is no big deal as machine learning is light years ahead now. But the what matters is making something by yourself, and learning something out of it and the joy that you get at the end of reaching the destination.

I did not add any bias to this example like the previous one because I was having a tough time making this without the bias, but it's better to have a bias and will add
The code is available here - https://gist.github.com/rukshn/361a54eaec0266167051d2705ea08a5f

From Biological Neuron To Perceptron

In the last post I wrote about how a biological neuron works, and in this post I'm going to write about perceptron and how to make one.

Basically the building block of our nervous system is the neuron which is the basic functional unit, it fires if it meets the threshold, and it will not fire if it doesn't meet the threshold. A perceptron is the same, you can call it the basic functional unit of a neural network. It takes an input, do some calculations and see if the output of reaches a threshold and fires accordingly.

A simple diagram of a perceptron  it takes two inputs x1 and x2 do some calculations f and gives an output

Perceptrons can only do basic classifications, these are called liner classifications it's like drawing a line and separating a set of data into two parts, it can't classify things the data into multiple classifications.

How a Perceptron Works

So the perceptron takes two inputs $x1$ and and $x2$, then they pass through the input nodes where they are multiplied by the respective weights. So the inputs $x1$ and $x2$ are like the stimulus to a neuron. 

And you must not forget that these $x1$ and $x2$ should be numbers, because they are being multiplied by weights (numbers) so there should be a way to convert a text input to a number representations, which is a different topic.

The inputs to the perceptron are the inputs multiplied by their weights, where inside the perceptron all these weights are added together.

So adding them all together

$$\sum\ f = (x1 * w1)+(x2 * w2)$$ 

And this sum then passes through an activation function, there are many activation functions and the ones used commonly are the hyperbolic tangent and the sigmoid function.

In this example I am using the sigmoid function.

$$S(t) = \frac{1}{1 + e^{-t}}$$

So the output of the perceotron is what comes out through the activation function.

How Perceotrons Learn?

Like I said before the perceptrons learn by adjusting their weights until it meets a desired output. This is done by a method called backpropagation.

In simple terms backpropagation is staring from calculating the error between the target and the output, and adjusting the weights backwards from the output weights, to hidden weights, to input weights (in a multilayered neural network).

In our simple perceptron it means adjusting the $w1$ and $w2$.

The equations and more details about backpropagation can be found here - https://web.archive.org/web/20150317210621/https://www4.rgu.ac.uk/files/chapter3%20-%20bp.pdf

Let's Make a Perceptron.

 

So we are going to make a perceptron, this won't do much and will only act as an 'AND' or 'OR' gate. The design of the perceptron is as same as the image above. I am using NodeJs but this can be done in a simpler way using Python and Numpy which I will hopefully set up on my computer to future use.

Let's take the AND gate first, the truth table for the AND gate is,

$$x=0 |  y = 0  | output = 0$$ 
$$x=1 |  y = 0  | output = 0$$
$$x=0 |  y = 1  | output = 0$$
$$x=1 |  y = 1  | output = 1$$

We are giving the the two inputs $x$ and $y$  and we are calculating the difference between the desired output and the output through our perceptron which is the error and backpropagating and adjusting the weights until the error becomes very small. This is called supervised learning.

So we are starting with two random values for the weights using Math.random() and then passing our first set of data of the truth table, then we calculate the error and backpropagate and adjust the weights just once, and then we present the second set of data and backpropagate and adjust the weights once and third set of data and the fourth set of data and so on, and the cycle is repeated.

Make sure you don't give the first set of data and adjust the weights till there is minimum error and then give the second set of data and adjust the weights till minimum error, this will not make the perceptron to learn all four patterns.

So I have repeated the cycle 10000 times and I plotted the error on a graph.

Error of 'and' gate changing over each time

 As you can see the error gets less and less and comes to a very low value, which is unnoticeable.

So now because the error is small means that the perceptron has been trained, so we an take that values of the weights, and feed the data of the truth table and see how close the perceptron's output is to the desired output.

Target and the output values of the perceotron in AND gate

 As you can see the perceptron has come pretty close to the target of the AND gate output.

We can do the same for the OR gate,

Starting with random values for weights and backpropagating like before until we get to the point of minimum error,

Error of 'or' gate changing over time

 And you can see that the OR gate perceptron has also come close to the desired target.

Target and output values of the perceptron in OR gate

 What about XOR?

$$x=0 |  y = 0  | output = 0$$ 
$$x=1 |  y = 0  | output = 1$$
$$x=0 |  y = 1  | output = 1$$
$$x=1 |  y = 1  | output = 0$$


You can see that the chart for the XOR is not as same as the ones we got for AND and OR gates, why is that?

Error of 'XOR' gate changing over time

Also we can see that the output for the XOR gate is also not correct?

Target and output values of the perceptron in XOR gate

So what is causing this error? Why can't the perceptron act as an XOR gate? how can we solve this? Hopefully I will answer that in a future post.

The code for the perceptron is available on here -  https://gist.github.com/rukshn/d4923e23d80697d2444d077eb1673e68

In the code you will see that there is a variable called bias,  bias is not a must but it is good to add a bias, in a $y = mx + c$ bias is the $c$. In a chart without the $c$ the line goes through $(0,0)$ but $c$ helps you to shift where the line, the bias is also the same. We bass bias as a fixed input to the with it's own weight which we adjust just like another weight using backpropagation.

Also the $\eta$ is called the learning factor, you can change it adjust the speed of learning, a moderate value is better.
 
 

How Does a Neuron Work?

So I was playing with some more machine learning and trying to make a perceptron from scratch again, I have to admit the one that I made few months back was somewhat buggy so I wanted to make something that works without errors.

Perceptron is the basic unit of a neural network just like the neuron which is the building block of our nervous system. So before talking about artificial neural networks I thought of writing about some physiology that I learned at first year of medical college. The physiological mechanism of a real neuron.

The neuron is the building block of our nervous system, there are nearly hundred billion neurons inside the human brain, that is a lot of neurons. How does so many neurons fit inside our head? One reason is that our brain is not flat, it had bumps, and ridges which increase the surface area of the brain which will make room for many more neurons as opposed to the brain being a flat hemispherical object.

The Structure

 

Although the brain different kinds types of neurons specialized for different functions, the basic structure is the same. It has a cell body, which has the nucleus and from the cell body comes out dendrites which connects with adjacent neurons, these dendrites brings signals towards the neuron (cell body).

And from the cell body comes out a long process called the axon, this axon can be few centimeters in length, it end by splitting in to small processes called axon terminals, which connect to adjacent dendrites. So the axon carries signals away from the neuron coming from the cell body.

Each neuron connects with nearly a thousand adjacent neurons, that is nearly hundred billion multiplied by thousand connections inside our human brain.

 

The Function

The way neurons work is based on electricity, the neurons outside is positively charged and the inside is negatively charged, the voltage difference between them is called the resting potential. It is the neutral state of a neuron. The main reason that outside is more positive is due to more sodium on the outside of the cell than inside.

And along the membrane of the neuron we have sodium channels, and when a stimulation is received these channels which is closer to the stimulation are opened and sodium which is abounded on the outside comes inside the cell causing the voltage difference to rise (making the inside of the cell more positive than the outside) and as more and more sodium comes in the voltage difference become, this depends on the strength of the stimulus.

So if the voltage difference passes a certain threshold then the neuron fires, casing an impulse to be carried along the axon to the adjacent neurons stimulating the ones connected to them. If the stimulus is not strong enough then the threshold is not reached and the neuron doesn't fire. This goes on until a desired action occurs in the body.

So coming back to the neuron, once the voltage difference rise to a certain level then another type of channels open on the cell membrane, these are potassium channels which pumps potassium from inside of the cell to outside.

So as more and more potassium is pumped outside the voltage difference becomes less and less because potassium is also a positively charge ion. So the voltage difference comes to the level of resting potential and goes even beyond the resting potential and comes to a period called absolute refractory period. Which means during a small time period no matter how strong the new stimulation is, it is not going to fire, but after sometime the voltage difference comes back to the resting potential and the neuron is ready for a new stimulus. And this cycle repeats itself.

So like I said before there are nearly hundred billion to thousand connections in the human brain, so how does the brain recognize patterns? This depends on the pattern of which neurons get activated by reaching the threshold and which neurons do not. It's like binary 0,0,1,1,1,0,0....0 will represent one pattern and the next binary code will represent another. This these are the things that we learn since our childhood and gets hard-coded in to our brain.

This is just a simplified version of how brain works, the brain has different areas for different functions like a part for processing visual data, a different area for processing audio and different area for processing language etc. So the brain is a complex machine that we are yet to understand.